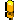AktuellesAktuelles
CM Storm Trigger im Härtetest	Plexiglas bearbeiten	NZXT - Adamas	NZXT - Apollo	Letzte Foren-BeiträgeLetzte Foren-Beiträge Re: Lang lebe das Modding-FAQ-Forum Re: "Lady Liberty" Re: "Lady Liberty" Re: "Lady Liberty" Re: "Lady Liberty" Re: "Lady Liberty"

Als Erstes möchten wir uns beim Forummitglied OlafSt, dem Autor des Artikels, bedanken. Vielen Dank nochmal. ;)

Für absolute Anfänger an dieser Stelle die Zusammenfassung wichtigster Bezeichnungen: U=Spannung, I=Strom(stärke) R=Widerstand. Und nun viel Spass!

Ein Spannungsteiler macht so ziemlich genau das, was sein Name schon preisgibt: Er teilt eine Gesamtspannung auf. Das ganze ist lächerlich einfach:

So sieht ein Spannungsteiler aus - eigentlich eine piepseinfache Reihenshaltung von Widerständen. Nun nehmen wir mal an, wir haben als VCC eine Spannung von 12V. Für R1 nehmen wir 1kOhm, für R2 nehmen wir 5kOhm.

Was passiert? Die Spannung teilt sich über den Widerständen gemessen im Verhältnis 1000:5000 oder auch 1:5 auf - ein Widerstand ist 5x größer als der andere. Daraus folgt logischerweise, die Spannung über R2 ist 5x größer als die Spannung über R1.

Hä? Warum das denn?

Das ist ebenso einfach erklärt: Der Strom muß auf seinem Weg vom Pluspol zum Minuspol durch die beiden Widerstände hindurch - wo sonst könnte er hinfließen?

Dem Strom ist es nun vollkommen Banane, ob er erst durch 1kOhm, dann durch 5kOhm oder gleich durch einen 6kOhm-Widerstand fließt. Aus diesem simplen Grund addieren sich die Widerstandswerte in einer Reihenschaltung. Anhand der simplen Formel R=U/I, wobei wir R und U kennen, kann man I errechnen:

I= U/R = 12V / 6000Ohm = 0,002A, also 2mA. Diese 2mA fließen durch beide Widerstände - er kann nirgendwo sonst lang.

Mit der gleichen Formel (R=U/I, wobei wir nun R und I zur Berechnung verwenden) können wir die Spannung, die an den einzelnen Widerständen stehenbleibt, ausrechnen:

U = R*I = 1000Ohm * 0,002A = 2V. Am R1 können wir also 2V messen.
U = R*I = 5000Ohm * 0,002A = 10V, Am R2 messen wir also 10V.

Wir sehen, die Spannung an R2 ist tatsächlich 5x größer als die über R1 ;-)

Neben dieser aufwändigen Art, das ganze auszurechnen, gibt es eine deutlich einfachere Methode:

• Wir addieren die Verhältnisse (5+1 = 6).
• Wir teilen die 12V durch 6, macht 2V. Diese 2V liegen über R1.
• Der Rest der 12V (oder auch das fünffache der 2V) liegen über R2: 10V.

Gegenrechnung: Die Summe der Spannungen über R1 und R2 muß wieder die Gesamtspannung ergeben: 2V + 10V = 12V.

Was messen wir nun wirklich an Punkt A? Das kommt darauf an:

• Klemmen wir das Voltmeter zwischen VCC (rote Meßleitung) und Punkt A (Punkt A betrachten wir einfach mal als Masse, also schwarze Meßleitung dran), dann messen wir 2V - das, was an R1 an Spannung stehen bleibt.
• Klemmen wir das Voltmeter zwischen Punkt A und Masse, messen wir 10V - das, was an R2 an Spannung stehenbleibt.

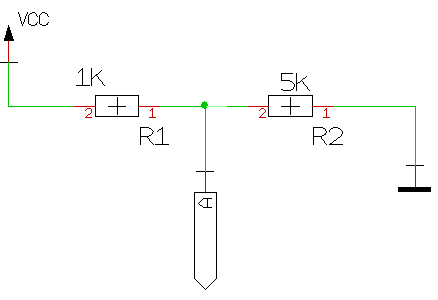
Das ganze funktioniert ebensogut, wenn wir die Widerstände vertauschen. Die Spannungen über den Widerständen bleiben dieselben. Wir messen nur plötzlich was anderes:

• Klemmen wir das Voltmeter zwischen VCC und Punkt A (Punkt A betrachten wir einfach mal als Masse), dann messen wir 10V - das, was an R1 (unserem Ex-R2) an Spannung stehen bleibt.
• Klemmen wir das Voltmeter zwischen Punkt A und Masse, messen wir 2V - das, was an R2 (unserem Ex-R1) an Spannung stehenbleibt.